2025-大发黄金版app下载

2025-01-11：求出最长好子序列ⅰ。用go语言，给定一个整数数组 nums 和一个非负整数 k，我们需要找出满足特定条件的子序列。

具体来说，如果一个整数序列 seq 在下标范围 [0, seq.length - 2] 内最多有 k 个下标 i 使得 seq[i] 不等于 seq[i 1]，我们就称这个整数序列为“好序列”。

我们的目标是返回数组 nums 中“好子序列”的最长长度。

1 <= nums.length <= 500。

1 <= nums[i] <= 1000000000。

0 <= k <= min(nums.length, 25)。

输入：nums = [1,2,1,1,3], k = 2。

输出：4。

解释：

最长好子序列为 [1,2,1,1,3] 。

答案2025-01-11：

题目来自leetcode3176。

1.定义一个名为 maximumlength 的函数，接收一个整数数组 nums 和一个非负整数 k 作为参数，返回最长好子序列的长度。

2.创建一个空间为 (k 1) 的整型数组 zd，用于存储最终的结果。

3.创建一个空的map dp，用于保存每个数字v（nums中的元素）对应的一个长度为 k 1 的动态数组。

4.遍历整数数组 nums，对于每个元素v，若该元素不在map中，则在map中新建一个k 1长度的数组。

5.对于当前元素v，从0到k遍历，利用动态数组 tmp 记录(i, j)的好子序列的长度为多少。

6.在内部遍历时，逐个更新 tmp 数组，如果j大于0，则比较 tmp[j] 的值和 zd[j-1] 1 的值的大小，取较大值。

7.在内部遍历结束后，更新 zd 数组，比较 zd[j] 和 tmp[j] 以及 zd[j-1] 的值，取较大值。

8.返回 zd[k]，即最终结果。

总的时间复杂度：

• 遍历整数数组 nums 需要o(n)的时间复杂度，其中n为nums数组的长度。

• 内部的循环在k范围内，所以是o(k)。

• 因此，总的时间复杂度为o(n*k)。

总的额外空间复杂度：

• 需要一个大小为 (k 1) 的数组 zd 存储结果，一个map dp 存储动态数组，一个长度为 k 1 的数组 tmp 用于临时存储好子序列长度。

• 所以总的额外空间复杂度为o(k)。

因此，根据所描述的操作和代码，整个算法的时间复杂度为o(n*k)，额外空间复杂度为o(k)，其中n为数组 nums 的长度，k为传入的非负整数k的值。

package main
import (
    "fmt"
)
func maximumlength(nums []int, k int) int {
    lennums := len(nums)
    dp := make(map[int][]int)
    zd := make([]int, k  1)
    for i := 0; i < lennums; i {
        v := nums[i]
        if _, ok := dp[v]; !ok {
            dp[v] = make([]int, k  1)
        }
        tmp := dp[v]
        for j := 0; j <= k; j {
            tmp[j]
            if j > 0 {
                tmp[j] = max(tmp[j], zd[j - 1]  1)
            }
        }
        for j := 0; j <= k; j {
            zd[j] = max(zd[j], tmp[j])
            if j > 0 {
                zd[j] = max(zd[j], zd[j - 1])
            }
        }
    }
    return zd[k]
}
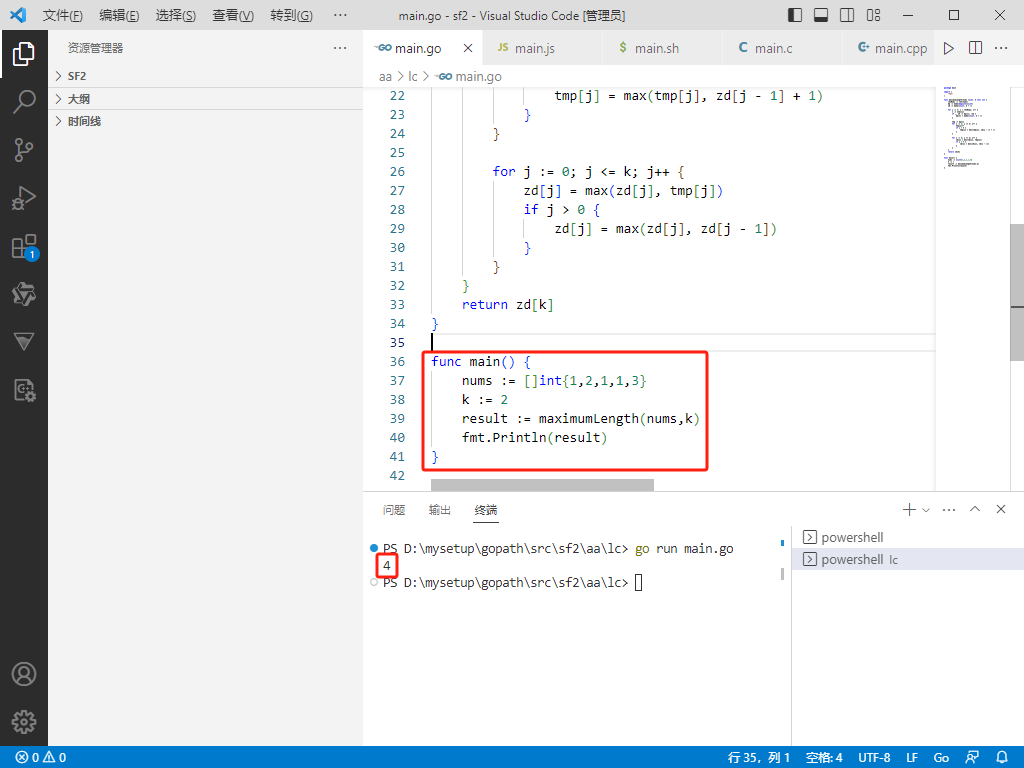
func main() {
    nums := []int{1,2,1,1,3}
    k := 2
    result := maximumlength(nums,k)
    fmt.println(result)
}

use std::collections::hashmap;
fn max(a: i32, b: i32) -> i32 {
    if a > b {
        a
    } else {
        b
    }
}
fn maximum_length(nums: vec<i32>, k: i32) -> i32 {
    let len_nums = nums.len();
    let mut dp: hashmap<i32, vec<i32>> = hashmap::new();
    let mut zd: vec<i32> = vec![0; (k  1) as usize];
    for i in 0..len_nums {
        let v = nums[i];
        if !dp.contains_key(&v) {
            dp.insert(v, vec![0; (k  1) as usize]);
        }
        let mut tmp = dp.get_mut(&v).unwrap();
        for j in 0..=k {
            tmp[j as usize]  = 1;
            if j > 0 {
                tmp[j as usize] = max(tmp[j as usize], zd[(j - 1) as usize]  1);
            }
        }
        for j in 0..=k {
            zd[j as usize] = max(zd[j as usize], tmp[j as usize]);
            if j > 0 {
                zd[j as usize] = max(zd[j as usize], zd[(j - 1) as usize]);
            }
        }
    }
    return zd[k as usize];
}
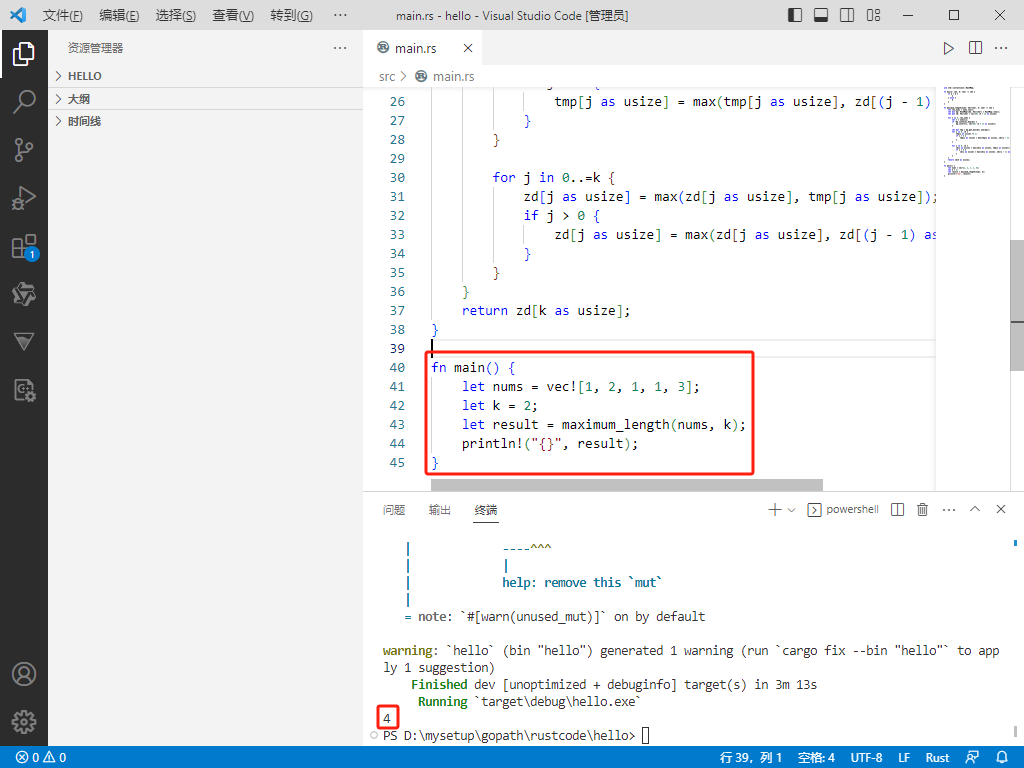
fn main() {
    let nums = vec![1, 2, 1, 1, 3];
    let k = 2;
    let result = maximum_length(nums, k);
    println!("{}", result);
}

#include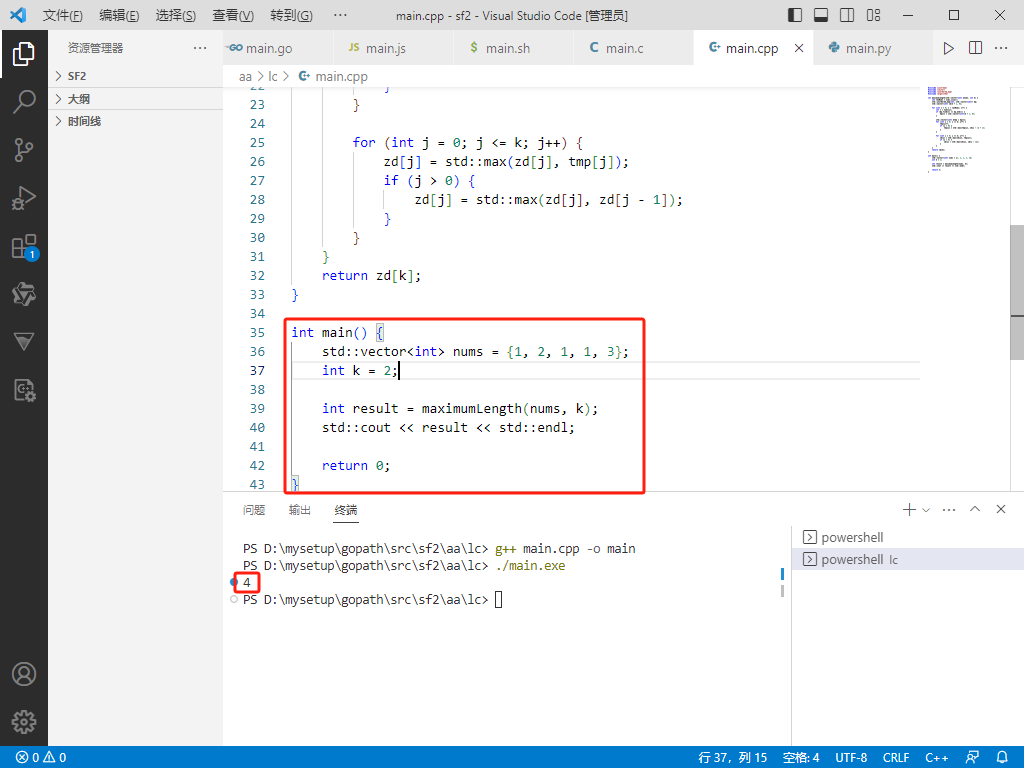 
#include 
#include 
#include 
int maximumlength(std::vector<int> &nums, int k) {
    int lennums = nums.size();
    std::unordered_map<int, std::vector<int>> dp;
    std::vector<int> zd(k  1, 0);
    for (int i = 0; i < lennums; i) {
        int v = nums[i];
        if (dp.find(v) == dp.end()) {
            dp[v] = std::vector<int>(k  1, 0);
        }
        std::vector<int> &tmp = dp[v];
        for (int j = 0; j <= k; j) {
            tmp[j];
            if (j > 0) {
                tmp[j] = std::max(tmp[j], zd[j - 1]  1);
            }
        }
        for (int j = 0; j <= k; j) {
            zd[j] = std::max(zd[j], tmp[j]);
            if (j > 0) {
                zd[j] = std::max(zd[j], zd[j - 1]);
            }
        }
    }
    return zd[k];
}
int main() {
    std::vector<int> nums = {1, 2, 1, 1, 3};
    int k = 2;
    int result = maximumlength(nums, k);
    std::cout << result << std::endl;
    return 0;
}

def maximum_length(nums, k):
    dp = {}
    zd = [0] * (k  1)
    for v in nums:
        if v not in dp:
            dp[v] = [0] * (k  1)
        tmp = dp[v]
        for j in range(k  1):
            tmp[j]  = 1
            if j > 0:
                tmp[j] = max(tmp[j], zd[j - 1]  1)
        for j in range(k  1):
            zd[j] = max(zd[j], tmp[j])
            if j > 0:
                zd[j] = max(zd[j], zd[j - 1])
    return zd[k]
if __name__ == "__main__":
    nums = [1, 2, 1, 1, 3]
    k = 2
    result = maximum_length(nums, k)
    print(result)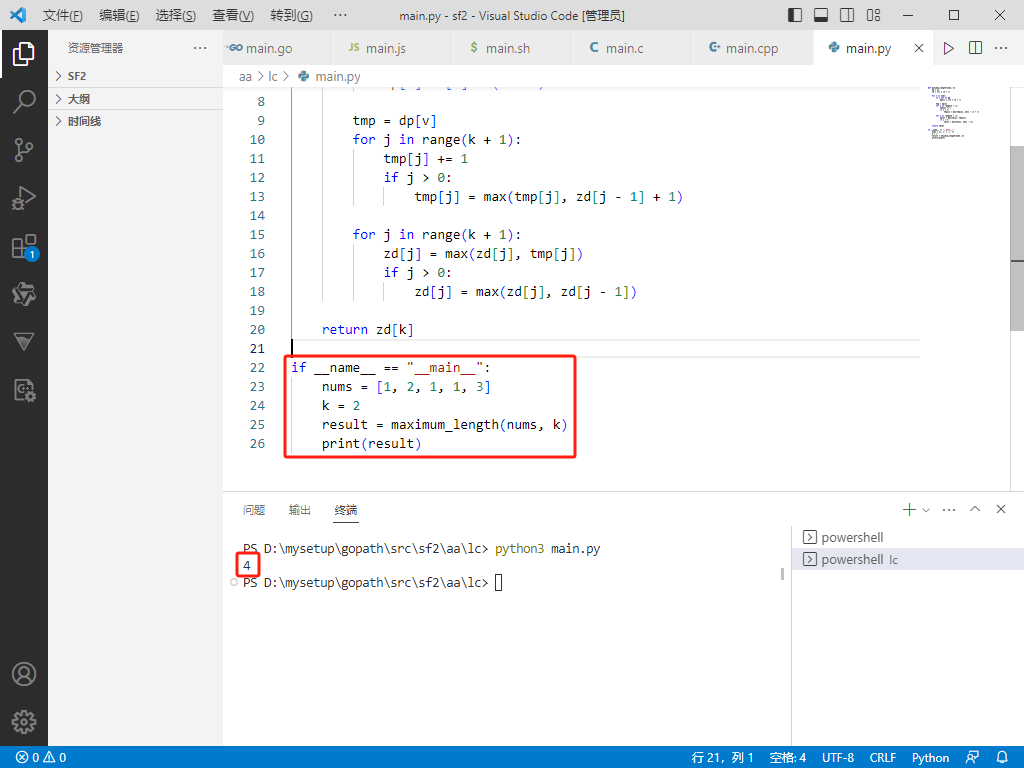

function maximumlength(nums, k) {
    let dp = {};
    let zd = new array(k  1).fill(0);
    for (let i = 0; i < nums.length; i) {
        let v = nums[i];
        if (!dp[v]) {
            dp[v] = new array(k  1).fill(0);
        }
        let tmp = dp[v];
        for (let j = 0; j <= k; j) {
            tmp[j];
            if (j > 0) {
                tmp[j] = math.max(tmp[j], zd[j - 1]  1);
            }
        }
        for (let j = 0; j <= k; j) {
            zd[j] = math.max(zd[j], tmp[j]);
            if (j > 0) {
                zd[j] = math.max(zd[j], zd[j - 1]);
            }
        }
    }
    return zd[k];
}
let nums = [1, 2, 1, 1, 3];
let k = 2;
let result = maximumlength(nums, k);
console.log(result);

本作品采用《cc 协议》，转载必须注明作者和本文链接